What are bandits?

A common situation in our research at Tiime is this:

• we have an algorithm that depends on hyperparameters;
• users provide discrete feedback (e.g., like/dislike or a star rating);
• we try to optimize the algorithm’s hyperparameters based on that feedback.

A natural approach to solving this problem is to use the multi-armed bandit model. In the simplest form, you draw independent samples from several random distributions (like “pulling an arm” of a slot machine).

The analogy is the following: the arms correspond to hyperparameter values, and pulling an arm corresponds to choosing that value when running the algorithm and collecting user feedback on the output.

It is obvious that the problem is easier when feedback is less random: with perfectly deterministic arms, one sample per arm suffices to identify the best.

A limitation of classic assumptions

However, most of the literature on multi-armed bandits just makes assumptions on the mean of the distributions.

This may seem odd at first glance since:

• less noise (including deterministic arms) should make the problem easier;
• less information should make the problem harder.

Yet mainstream papers largely sidestep this. A possible reason is that it is not easy to quantify what noise is. The best definition I know comes from a finance paper by Rothschild and Stiglitz (1970), and to my knowledge, it has not been used in the bandit literature.

Less information is also not easy to quantify, but it gets interesting when we consider a particular case of arms with “less information”: discrete feedback.

In our experience, some optimization algorithms on continuous hyperparameters actually break when feedback is too sparse. An obvious way to mitigate this is to collect feedback in batches of, e.g., 10 samples and return the mean of the batch as a continuous signal. However, we can ask a more general question:

How much harder is learning from discrete feedback than from continuous feedback?

To illustrate, we start from a continuous distribution and discretize it so that we can compare the convergence of bandit algorithms in both cases. It is fair to compare these two distributions since the discrete one is a discretization of the continuous one.

Now, this is a blog post, not a research paper, so I will demonstrate a specific case to build intuition. We make the following assumptions:

• We focus on best-arm identification: we want to identify which distribution (“arm”) is best; we do not optimize cumulative reward.
• We compare two distributions, either both continuous or both discrete.
• The continuous distributions $A$ and $B$ are normal distributions with means $\delta$ and $-\delta$ and variance $1$ (without loss of generality).
• The discrete distributions $A’$ and $B’$ are, respectively, the signs of samples from $A$ and $B$, i.e., they are Bernoulli with parameters $\Phi(\delta)$ and $\Phi(-\delta)$.

The advantage of best-arm identification with two arms is that it is solved:

We would like to mention that the case K = 2 is unique and simple since, as we will indirectly see, it is optimally solved by the uniform allocation strategy consisting in drawing each arm n times, and at the end recommending the arm with the highest empirical mean.

Taking the sign to obtain the discrete distributions is also not an arbitrary choice: because our means are $\pm \delta$, I claim it is the best binary discretization to separate the two distributions (of course, one should prove that no other binary function yields a smaller probability of error).

r/TheyDidTheMath

What is the error probability of the optimal strategy in both cases? This should tell us how much harder it is to learn from discrete feedback than from continuous feedback.

Continuous case

We define the sample means of $A$ and $B$ as $X$ and $Y$, respectively.

$X$ and $Y$ are normally distributed with means $\delta$ and $-\delta$ and variance $1/n$.

The probability of error is $P(X < Y) = P(X - Y < 0)$.

The distribution of $X - Y$ is normal with mean $2\delta$ and variance $2/n$.

Thus, the probability of error is:

where $\Phi$ is the cumulative distribution function of the standard normal distribution.

import numpy as np
from scipy.stats import norm

def continuous_error(n, delta):
    return norm.cdf(-delta * np.sqrt(2 * n))

Discrete case

We define $X$ and $Y$ as the sums (instead of the means, which only rescales and makes the math easier) of the binary signs ($0$ for negative, $1$ for positive) of $n$ samples from $A’$ and $B’$, respectively.

The probability of getting $1$ when sampling from $A’$ (resp. $B’$) is $P(A’ = 1) = P(A > 0) = \Phi(\delta)$ (resp. $P(B’ = 1) = P(B > 0) = \Phi(-\delta)$).

Thus, $X$ and $Y$ are binomially distributed with parameters $n$ and $p=\Phi(\delta)$ (resp. $q=\Phi(-\delta)=1-p$).

The probability of error is $P(X < Y) + \tfrac{1}{2}P(X = Y)$ because we have to account for ties.

We can compute the probability of error with the following simple Python snippet:

import numpy as np
from scipy.stats import norm, binom

def discrete_error(n, delta):
    p = norm.cdf(delta)
    q = 1 - p
    # P(X < Y)
    y = np.arange(1, n + 1)
    p_lt = np.sum(binom.pmf(y, n, q) * binom.cdf(y - 1, n, p))
    # 0.5 * P(X = Y)
    k = np.arange(n + 1)
    p_eq = np.sum(binom.pmf(k, n, p) * binom.pmf(k, n, q))
    return p_lt + 0.5 * p_eq

When $n$ is large, $X-Y$ is approximately normal with mean $n(p-q)$ and variance $2npq$.

Thus, the probability of error is $P(X-Y < 0)$ (ties vanish asymptotically), which is $\Phi\left(\tfrac{n(q-p)}{\sqrt{2npq}}\right)$.

def discrete_error_approx(n, delta):
    p = norm.cdf(delta)
    q = 1 - p
    return norm.cdf(n * (q - p) / np.sqrt(2 * n * p * q))

Let’s plot these curves for different values of $n$ and $\delta$:

import matplotlib.pyplot as plt

ns = np.arange(1, 200)
deltas = [0.1, 0.2, 0.5]

fig, axes = plt.subplots(1, 3, figsize=(12, 4))
for ax, delta in zip(axes.flatten(), deltas):
    ax.plot(ns, [continuous_error(n, delta) for n in ns], label="Continuous")
    ax.plot(ns, [discrete_error(n, delta) for n in ns], label="Discrete")
    ax.plot(
        ns,
        [discrete_error_approx(n, delta) for n in ns],
        label="Discrete (approx)",
        linestyle="--",
    )
    ax.set_yscale("log")
    ax.legend()
    ax.set_title(f"$\\delta = {delta}$")
    ax.set_xlabel("Number of samples")
    ax.set_ylabel("Probability of error")

plt.tight_layout()
plt.show()

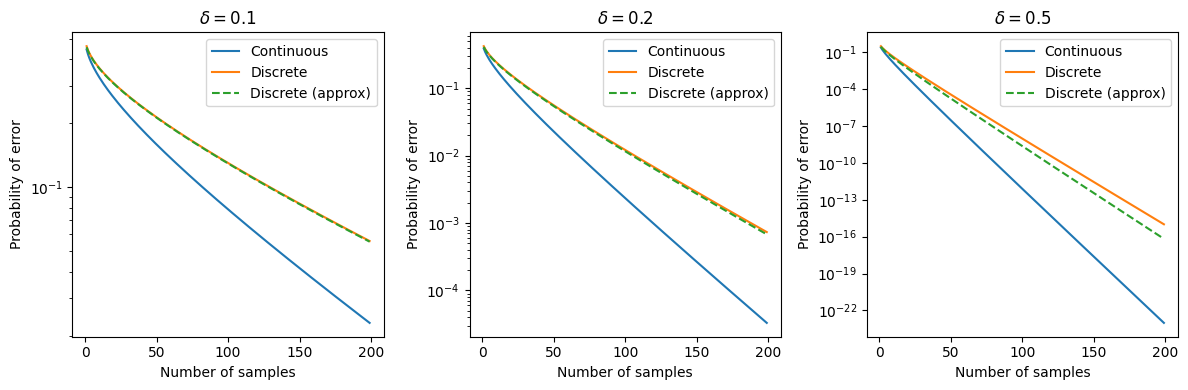
When $\delta$ is small (i.e., when the distributions are very close—which is the interesting case), the normal approximation for the discrete case is very accurate.

Discrete bandits are $\frac{\pi}{2}$ times harder (in this example)

Let $f(n)$ denote the probability of error in the continuous case and $g(n)$ the probability of error in the discrete case.

We have:

Let’s find out how much harder it is to learn from discrete feedback than from continuous feedback—that is, the effective value of $n$ that gives the same probability of error as the continuous case. We solve:

Solving yields:

When $\delta$ is small, we have

Thus \(\frac{4\,\delta^{2}\,p(1-p)}{(2p-1)^2} = \frac{\pi}{2} - \delta^2 \approx \frac{\pi}{2}.\)

Let’s plot the curves for different values of $n$ and $\delta$:

ns = np.arange(1, 1000)
deltas = [0.1, 0.2, 0.5]

fig, axes = plt.subplots(1, 3, figsize=(12, 4))
for ax, delta in zip(axes.flatten(), deltas):
    ax.plot(
        ns,
        [continuous_error(n, delta) for n in ns],
        label="Continuous",
        linestyle="-",
    )
    ax.plot(
        ns,
        [discrete_error(int(n * np.pi / 2), delta) for n in ns],
        label="Discrete at $n_{eff}$",
        linestyle="--",
    )
    ax.set_yscale("log")
    ax.legend()
    ax.set_title(f"$\\delta = {delta}$")
    ax.set_xlabel("Number of samples")
    ax.set_ylabel("Probability of error")

plt.tight_layout()
plt.show()

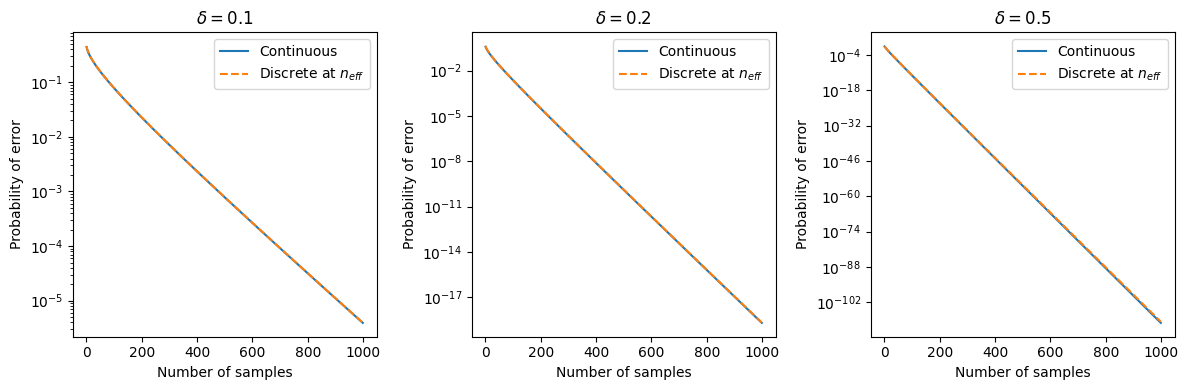
Yup, the math is correct.

Conclusion

In this two-arm, best-arm identification setting with Gaussian rewards, converting continuous feedback to binary feedback (by taking the sign) incurs a fixed and interpretable cost: you need about a factor of $\tfrac{\pi}{2} \approx 1.57$ more samples to achieve the same error probability. In practice, this does not affect the asymptotic convergence rate of the algorithm which is why I think it is not mentioned in the literature. However it is still a good thing to know!