Cryptography brings a lot of counterintuitive results. The most famous is the Diffie–Hellman key exchange that shows that two persons who can only send information publicly are able to share a secret. This shared secret can then be used to encrypt any message.

I would like to share some thoughts about another, more niche, use of cryptography to share secrets: verifiable encryption.

Imagine that Alice possesses a secret that Bob wants to buy. Bob knows what he wants to buy because he possesses a fingerprint, like a cryptographic hash. Alice also wants to be sure that Bob cannot claim that she did not send the correct secret, and that she will not need to reveal the secret to a verifying third party. Thus, Alice is going to encrypt the secret such that anyone can check that it corresponds to the fingerprint. This is called verifiable encryption.

A practical application of verifyable encryption would be to attach secret data to NFTs. A NFT is basically like a marriage in which everyone in the world is banging your wife, and you can’t do anything about it, but you do have the marriage certificate, so that’s cool. With verifiable encryption, one could create a NFT such that each owner has to transfer the same secret to the next owner. Of course, previous owners would still have access to the secret and nothing would prevent them from publicly revealing it.

Another practical use would be a decentralized DRM (digital rights management) system. CAO21 describes such a system using zero-knowledge proofs.

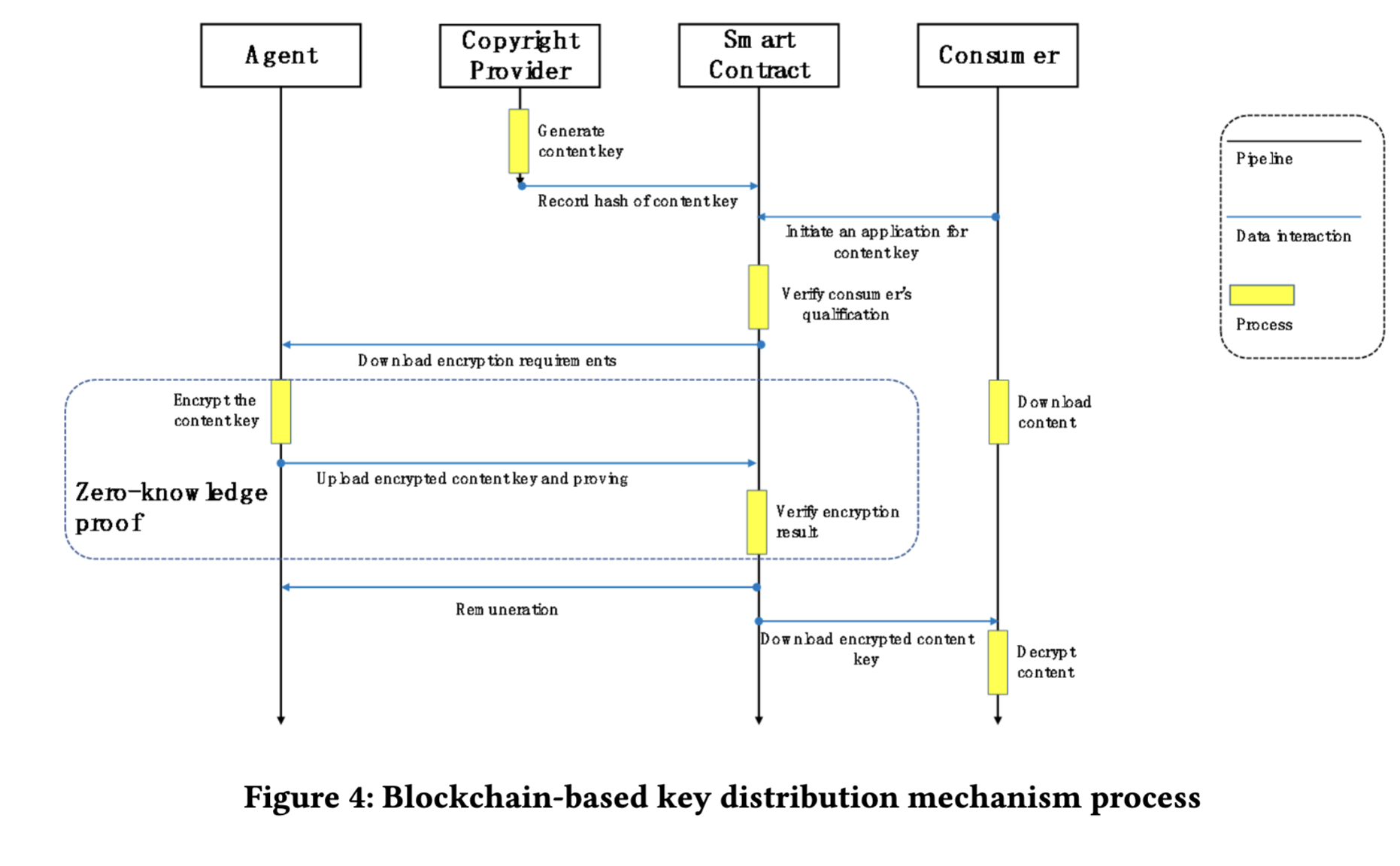
Zero-knowledge proofs are another super powerful card in the cryptographic toolbox: they allow a prover to justify that they know a secret that satisfies some properties that are known to a verifier without making the verifier able to learn anything about the secret. In their most powerful form, any computation can be made to check the properties, so they are an obvious answer to our problem: Alice can simply emit a proof that she knows a secret such that hash(secret) == fingerprint and encryption(secret) == message. If you want to learn more about the ZKP ecosystem, I found this super cool page.

This paper made me question the practicality of verifiable encryption and the possibility to use simpler methods.

First, zero-knowledge proofs are relatively complicated because they are general. They do make a lot of sense to check hash values because cryptographic hashes are arbitrary circuits. But we can choose a mathematically simpler one-way function, like exponentiation in a group. That method relies on the assumption that the discrete logarithm is hard to compute. In such a setting, the verifier checks secret * G == fingerprint, where G is the group generator, and encryption(secret) == message (note that we use the multiplicative notation to match the conventions of elliptic curves). A classical scheme for discrete logarithm proofs was described in CAM03, but it relies on the strong RSA assumption, so it now requires quite large parameters. Another is Juggling from JUG20 and is implemented there. Juggling is more general as it allows transferring segments of the discrete logarithm but it is quite complicated as it relies on other building blocks like bulletproofs. I asked if there was a simple method and there is actually one that I will explain below. Let us call it the ECC (for Elliptic Curve Cryptography) method. Although both methods involve ECC, this one does not require much more.

The other thing I was curious about is how practical it would be to use zero-knowledge proofs with hashes. Let us call that method ZK (for zero-knowledge). On blockchains, operations are made using smart contracts. Those smart contracts are executed on a lot of computers, thus their operations generate transaction fees measured in gas. The question is thus: how much gas do the ECC and ZK methods consume in a typical exchange?

I implemented both systems and made the code available on github.

How the ECC method works

We are going to use elliptic curves. All you need to know is that we rely on a group with generator $G$. Capital letters (eg $A$) denote multiplications of $G$ by the associated lowercase letter (eg $a G$). Since we suppose that the discrete logarithm problem is hard, the multiplication operation is simple but one-way: it is easy to compute $a \rightarrow A$ but impossible to compute $A \rightarrow a$. In the vocabulary of asymetric cryptography, a random $a$ can be used as a private key and $B$ as a public key.

The secret is $m$ and its fingerprint is $M := m G$.

The ECC method works in three steps:

1. Alice sends her public key $A$ to Bob.
2. Bob encrypts a random blinding scalar $b$ with $A$ and sends $Enc(A, b)$ and $B$ to Alice
3. Alice sends $c = m + b$ to Bob.

Nobody can learn anything from $m + b$ because it is uniformly distributed. However, anyone can check that $C = (m+b) G$ is equal to $M + B$.

This protocol is quite simple, with the little drawback that it requires 3 messages and that Bob could cheat in step 2. If Alice claims that Bob sent a wrong value of $b$, Bob can just publish it as it has no value.

Here is the full code, taken from the test file:

Public = Namespace()
Alice = Namespace()
Bob = Namespace()
total_gas = 0

Alice.m = make_secret()
Public.M = curve25519(Alice.m, include_y=True)

Alice.a = make_secret()
Public.xA = curve25519(Alice.a)

alice = accounts[0]
bob = accounts[1]
amount = "10 ether"
escrow = eccEscrow.deploy(Public.M, Public.xA, bob, amount, {"from": alice})
print("Deployment used", escrow.tx.gas_used)
total_gas += escrow.tx.gas_used

# Bob generates a secret `b` and publishes `B`.
Bob.b = make_secret()
Public.B = Public.xB, _ = curve25519(Bob.b, include_y=True)

# Bob sends `b` securely to Alice using ECIES
# https://en.wikipedia.org/wiki/Integrated_Encryption_Scheme
Bob.salt = make_secret()
Public.m1 = ecies_encrypt(Bob.b, Bob.salt, Public.xA)

tx = escrow.bob(Public.B, *Public.m1, {"from": bob, "value": amount})
print("Bob used", tx.gas_used)
total_gas += tx.gas_used

# Alice checks that `B` is valid
assert valid(*Public.B)
# Alice decrypts `b` and checks that it corresponds to B
Alice.b = ecies_decrypt(Public.m1, Alice.a)
assert curve25519(Alice.b) == Public.xB, "A claims the value is false"

# If Alice claims that the value is false, Bob can make `salt` public
Public.salt = Bob.salt
assert ecies_check(Public.xA, Public.m1, Public.xB, Public.salt)
del Public.salt

# Alice publishes m2
Public.m2 = (Alice.m + Alice.b) % ORDER

tx = escrow.alice(Public.m2, {"from": alice})
print("Alice used", tx.gas_used)
total_gas += tx.gas_used

Bob.m = normalize_secret(Public.m2 - Bob.b)

# Bob has got the correct secret
assert Bob.m == Alice.m
# Anyone can see that m was sent to Bob
assert curve25519(Public.m2, include_y=True) == add(Public.M, Public.B)

print("Total gas used", total_gas)

We used Daniel J. Bernstein’s Curve25519 and a simple version of the Elliptic Curve Integrated Encryption Scheme without MAC and using XOR as encryption. It is quite similar to ElGamal encryption with a call to the Keccak hashing function:

def ecies_encrypt(secret, salt, xPub):
    return curve25519(salt), secret ^ keccak256(mult(salt, xPub))


def ecies_decrypt(msg, a):
    public_salt, msg = msg
    return msg ^ keccak256(mult(a, public_salt))


def ecies_check(public_key, msg, fingerprint, salt):
    public_salt, msg = msg
    secret = msg ^ keccak256(mult(salt, public_key))
    return curve25519(salt) == public_salt and curve25519(secret) == fingerprint

ecies_check can be used to verify that $Enc(A, b)$ is correct. It actually takes salt as input and not secret because it is possible to retrieve secret from salt and msg. However, the encrypted message contains public_salt := salt * G hence we need salt to check that public_salt is correct.

Finally, we implemented the necessary curve25519 operations in a Solidity smart contract, allowing us to code the final call as:

function alice(uint256 m2) public {
    require(msg.sender == Alice);
    require(_curve25519(m2) == _add(M[0], M[1], B[0], B[1]));
    payable(Alice).transfer(address(this).balance);
}

How the ZK method works

The ZK protocol is conceptually simpler, thanks to most of the complexity being hidden in the ZoKrates compiler.

The zero-knowledge proofs as implemented in ZoKrates do not actually take a general program as input but a sequence of primitive operations. These are then compiled to something called a rank-1 constraint system (R1CS) which is a set of linear equations. This system of constraints is standard and can then be used to produce proofs with cryptographic primitives, like zkSNARKs or bulletproofs.

Instead of programming with primitive operations, which would be the equivalent of coding in assembly, ZoKrates uses a DSL (domain-specific language) and implements a few useful functions, like hashes and elliptic curve operations.

The protocol is much simpler because all we have to do is provide a proof that we encrypted correctly.

We are going to use the same encryption mechanism as above:

def ecies_encrypt(secret, salt, xPub):
    return curve25519(salt), secret ^ keccak256(mult(salt, xPub))

However, instead of curve25519, we are going to use Baby Jubjub as it is already implemented.

Proving that the encryption works is almost the same process as ecies_check above:

def ecies_check(public_key, msg, fingerprint, salt):
    public_salt, msg = msg
    secret = msg ^ keccak256(mult(salt, public_key))
    return curve25519(salt) == public_salt and curve25519(secret) == fingerprint

The only difference is that the fingerprint is not secret * G but hash(secret).

The actual circuit is defined by this very short code:

def main<use_keccak>(
    field salt,
    u32[8] fingerprint,
    field[2] public_key,
    u32[8] msg,
    field[2] public_salt
    ) {
    
    bool[256] saltbin = unpack256(salt);
    assert(mult(saltbin, generator, BABYJUBJUB_PARAMS) == public_salt);

    bool[256] tmp = compress(mult(saltbin, public_key, BABYJUBJUB_PARAMS));
    u32[8] mask = if (use_keccak != 0) {keccak(tmp)} else {sha256Padded(tmp)};

    u32[8] mut secret32 = [0; 8];
    for u32 i in 0..8 {
        secret32[i] = msg[i] ^ mask[i];
    }
    bool[256] secret = u32_8_to_bool_256(secret32);

    u32[8] hash = if (use_keccak != 0) {keccak(secret)} else {sha256Padded(secret)};
    assert(hash == fingerprint);

    return;
}

This generic code that can call two different hash functions is then used like this:

import "../template" as aux;

def main(
    private field salt,
    u32[8] fingerprint,
    field[2] public_key,
    u32[8] msg,
    field[2] public_salt
    ) {
    
    return aux::<1>(salt, fingerprint, public_key, msg, public_salt);
}

As you can see, salt is marked private, which means that it is a secret that we want to prove we know.

Deployment involves a few command-line calls that are make from Python by this file:

• zokrates compile to produce the circuit from the code
• zokrates setup to generate proving and verification keys
• zokrates export-verifier to produce the Solidity verifier
• zokrates compute-witness and zokrates generate-proof to produce the proof

A little flaw of zkSNARKs compared to bulletproofs is that they require setup to be done by a third party that is trusted to delete some data that could be used to generate fake proofs. In principle, the setup should thus be performed by a trusted entity that can then publish the keys. Multiple entities can also do it using multiparty computation as explained here.

In our case, we are going to suppose that a trusted third party called Eve deployed the verifier.

The smart contract looks like this:

contract zkEscrow_keccak {
    uint32[8] public fingerprint;
    uint256[2] public publicKey;
    uint256 public amount;
    address public verifier;

    constructor(
        address _verifier,
        uint32[8] memory _fingerprint,
        uint256[2] memory _publicKey
    ) payable {
        // Bob inits and pays the price
        verifier = _verifier;
        fingerprint = _fingerprint;
        publicKey = _publicKey;
        amount = msg.value;
    }

    function alice(
        uint32[8] calldata message,
        uint256[2] calldata public_salt,
        Verifier.Proof calldata proof
    ) external {
        uint[20] memory input;
        for (uint i = 0; i < 8; i++) input[i] = fingerprint[i];
        for (uint i = 0; i < 2; i++) input[i + 8] = publicKey[i];
        for (uint i = 0; i < 8; i++) input[i + 10] = message[i];
        for (uint i = 0; i < 2; i++) input[i + 18] = public_salt[i];
        if (!Verifier(verifier).verifyTx(proof, input)) revert();
        payable(msg.sender).transfer(amount);
    }
}

Notice that the verifier can be reused in multiple escrows.

Here is the full code, taken from the test file:

Public = Namespace()
Alice = Namespace()
Bob = Namespace()
total_gas = 0

# Alice wants to send a secret `secret` with  hash `fingerprint` to Bob.
Alice.secret = random.randrange(2**256)
Public.fingerprint = hash(Alice.secret)

Bob.private_key = PrivateKey.from_rand()
Public.public_key = PublicKey.from_private(Bob.private_key)

alice = accounts[0]
bob = accounts[1]
eve = accounts[2]
amount = "10 ether"

verifier = Verifier.deploy({"from": eve})
escrow = zkEscrow.deploy(
    verifier.address,
    int_to_u32_array(Public.fingerprint),
    [Public.public_key.p.x.n, Public.public_key.p.y.n],
    {"from": bob, "value": amount},
)
print("Deployment used", escrow.tx.gas_used)
total_gas += escrow.tx.gas_used

Alice.salt = PrivateKey.from_rand()
Public.public_salt = PublicKey.from_private(Alice.salt)

Alice.mask = hash(Public.public_key.p.mult(Alice.salt.fe).compress())
Public.msg = Alice.secret ^ Alice.mask

proof = prove(
    name,
    [
        Alice.salt.fe.n,
        int_to_u32_array(Public.fingerprint),
        [Public.public_key.p.x.n, Public.public_key.p.y.n],
        int_to_u32_array(Public.msg),
        [Public.public_salt.p.x.n, Public.public_salt.p.y.n],
    ],
)

tx = escrow.alice(
    int_to_u32_array(Public.msg),
    [Public.public_salt.p.x.n, Public.public_salt.p.y.n],
    (proof["proof"]["a"], proof["proof"]["b"], proof["proof"]["c"]),
    {"from": alice},
)
print("Alice used", tx.gas_used)
total_gas += tx.gas_used

# Bob decrypts the message
Bob.mask = hash(Public.public_salt.p.mult(Bob.private_key.fe).compress())
Bob.secret = Public.msg ^ Bob.mask

# Bob has got the correct secret
assert Bob.secret == Alice.secret

print("Total gas", total_gas)

Results

Here is the output of pytest -s:

tests/test_ecc.py::test RUNNING
Deployment used 653150
Bob used 105392
Alice used 726963
Total gas used 1485505
tests/test_ecc.py::test PASSED

tests/test_zk.py::test_zk_sha256 RUNNING
Verifier deployment used 1412632
Escrow deployment used 480814
Alice used 438172
Total escrow gas 918986
Total gas 2331618
tests/test_zk.py::test_zk_sha256 PASSED

tests/test_zk.py::test_zk_keccak RUNNING
Verifier deployment used 1412632
Escrow deployment used 480802
Alice used 438208
Total escrow gas 919010
Total gas 2331642
tests/test_zk.py::test_zk_keccak PASSED

The ECC method is cheaper overall, using about 1.5M gas.

The ZK method is a bit more expensive at 2.3M, but using sha256 or keccak as hash function has no impact on the cost, which is good to know. Most of the cost is due to the Verifier deployment. I guess the ECC deployment could be cheaper if we included the Curve25519 functions in another contract.

Hence, if we look at just the cost of verification, ZK costs 400k while ECC costs 700k.